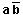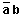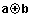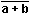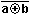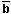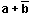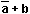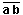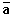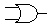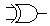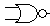Fonctions logiques

La fonction logique d'un circuit combinatoire peut se définir par le tableau de correspondance entre les états d'entrée et les états de sortie
Pour n variables il y a 2²ⁿ fonctions possibles

0    0	0    1	1    0	1    1	a b
0	0	0	0	F0 = 0 ( constante nulle )
0	0	0	1	F1 = a b ( fonction ET )
0	0	1	0	F2 =
0	0	1	1	F3 = a
0	1	0	0	F4 =
0	1	0	1	F5 = b
0	1	1	0	F6 = ( fonction XOR )
0	1	1	1	F7 = a + b ( fonction OU )
1	0	0	0	F8 = ( fonction NOR )
1	0	0	1	F9 =
1	0	1	0	F10 =
1	0	1	1	F11 =
1	1	0	1	F13 =
1	1	1	0	F14 = ( fonction NAND )
1	1	1	1	F15 = 1 ( constante 1 )

Il est possible montrer que toutes fonctions booléennes d'un nombre quelconque de variables peut s'écrire avec les trois fonctions de base ET, OU et NON

a NON ( NOT ) a b a b ET ( AND ) a b a + b OU ( OR )

a b XOR a b NAND a b NOR